Confusion about Polygon orientation

febedtu · October 12, 2022, 2:49pm

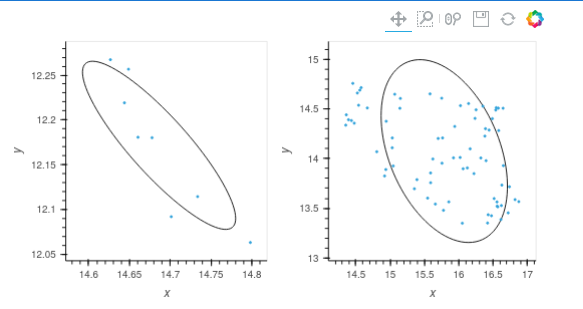
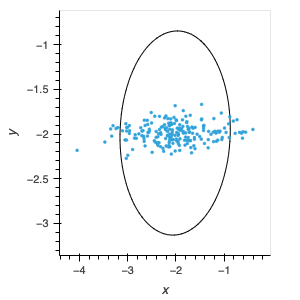
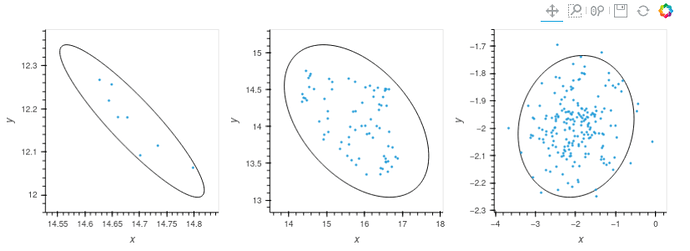
I would like to encircle my scatter plot data with a measure of standard deviation. Unfortunately I can’t seem to get the orientation setting right. I am confused by the available descriptions:

Orientation in the Cartesian coordinate system, the
counterclockwise angle in radians between the first axis and the
horizontal
and
you can set the orientation (in radians, rotating anticlockwise)

My script and data example:

def eigsorted(cov):
    vals, vecs = np.linalg.eigh(cov)
    order = vals.argsort()[::-1]
    return vals[order], vecs[:,order]

def encircle(x, y, nstd = 3):
    cov = np.cov(x, y)
    vals, vecs = eigsorted(cov)
    theta = np.degrees(np.arctan2(*vecs[:,0][::-1]))
    w, h = 2 * nstd * np.sqrt(vals)
    return h, w, theta

def list_polygon(_dict):
    list_polygons = []
    for key in _dict.keys():
        _polygon = hv.Polygons([{('x', 'y'): hv.Ellipse(np.mean(_dict[key][0]), np.mean(_dict[key][1]), (_dict[key][2], _dict[key][3]), orientation=(_dict[key][4]**0.01745)).array()}]).opts(color=_dict[key][5])
        # _polygon = hv.Ellipse(_dict[key][0], _dict[key][1], (_dict[key][2], _dict[key][3]), (_dict[key][4]/360)*np.pi).opts(color=_dict[key][5])
        list_polygons.append(_polygon)
    return list_polygons



array_0_x = [14.626729965209961, 14.648904800415039, 14.733654975891113, 14.798286437988281, 14.643913269042969, 14.677755355834961, 14.66055965423584, 14.70136833190918]
array_0_y = [12.267253875732422, 12.25666618347168, 12.114402770996094, 12.063163757324219, 12.219114303588867, 12.180122375488281, 12.18067741394043, 12.09195613861084]
array_0_h, array_0_w, array_0_theta = encircle(x = array_0_x, y = array_0_y, nstd = 3)

array_1_x = [16.06388282775879, 16.12518882751465, 15.923401832580566, 16.020185470581055, 15.066932678222656, 15.149603843688965, 14.54041862487793, 14.667778015136719, 15.142616271972656, 16.650007247924805, 16.62876319885254, 14.558774948120117, 14.456321716308594, 16.539690017700195, 16.380924224853516, 16.166292190551758, 16.25292205810547, 16.322223663330078, 16.442623138427734, 15.941734313964844, 16.143335342407227, 15.581430435180664, 15.751699447631836, 16.820762634277344, 16.720598220825195, 14.522720336914062, 14.577762603759766, 16.8760929107666, 16.73967742919922, 16.02482032775879, 16.420291900634766, 16.490720748901367, 16.23689842224121, 16.389381408691406, 16.352201461791992, 16.477752685546875, 16.428762435913086, 16.615528106689453, 16.56000328063965, 16.546770095825195, 16.576906204223633, 16.646148681640625, 16.582895278930664, 15.764276504516602, 15.700431823730469, 14.943675994873047, 14.805766105651855, 14.361465454101562, 14.47752571105957, 16.05176544189453, 15.777639389038086, 14.393733024597168, 14.353582382202148, 15.59047794342041, 15.354070663452148, 16.22173309326172, 16.398263931274414, 15.546730041503906, 15.855430603027344, 14.920063018798828, 15.045196533203125, 15.030611038208008, 15.031574249267578, 15.65877628326416, 14.43680191040039, 14.937338829040527, 15.756300926208496, 15.589689254760742, 15.390737533569336, 15.623208045959473, 16.569225311279297, 16.62229347229004, 16.51552963256836, 16.557403564453125]
array_1_y = [13.897571563720703, 13.906061172485352, 14.007840156555176, 14.011129379272461, 14.648042678833008, 14.606070518493652, 14.537391662597656, 14.50973892211914, 14.506791114807129, 13.92885684967041, 13.733349800109863, 14.689118385314941, 14.757230758666992, 14.488571166992188, 14.226333618164062, 14.098344802856445, 14.49145221710205, 14.006555557250977, 14.287406921386719, 14.323968887329102, 14.55444049835205, 14.651986122131348, 14.60823917388916, 13.58717155456543, 13.453489303588867, 14.660158157348633, 14.714993476867676, 13.566643714904785, 13.716506004333496, 14.53334903717041, 13.351394653320312, 14.401777267456055, 14.404946327209473, 14.301204681396484, 14.527425765991211, 13.424491882324219, 13.43462085723877, 13.386327743530273, 13.521247863769531, 14.512731552124023, 14.508121490478516, 14.507160186767578, 14.282684326171875, 14.207962989807129, 14.202638626098633, 14.375961303710938, 14.069111824035645, 14.440964698791504, 14.35629940032959, 13.349201202392578, 13.479074478149414, 14.391450881958008, 14.337162971496582, 13.757364273071289, 13.696568489074707, 13.849023818969727, 13.97883415222168, 13.602248191833496, 13.564446449279785, 13.82508659362793, 13.92595386505127, 14.109186172485352, 14.207939147949219, 13.542155265808105, 14.383004188537598, 13.889872550964355, 13.953922271728516, 13.855619430541992, 13.788017272949219, 13.995970726013184, 13.514547348022461, 13.527362823486328, 13.59772777557373, 13.563745498657227]
array_1_h, array_1_w, array_1_theta = encircle(x = array_1_x, y = array_1_y, nstd = 3)


_dict = {0: [array_0_x,
  array_0_y,
  array_0_h,
  array_0_w,
  array_0_theta,
  'rgba(31,119,180,0.5)'],
 1: [array_1_x,
  array_1_y,
  array_1_h,
  array_1_w,
  array_1_theta,
  'rgba(31,119,180,0.5)']}

list_polygons = list_polygon(_dict)
hv.Overlay(list_polygons) * hv.Points((array_0_x, array_0_y)) * hv.Points((array_1_x, array_1_y))

Hoxbro · October 12, 2022, 3:54pm

I could not get your code to run. But if I use your data, I can get the desired plot (I haven’t double-checked the code, so there could be some small bugs).

Things I have done differently from you is to not convert the angle into degrees and keep it in radians and calculate the standard deviation after I turn the data around for each direction. Without calculating it for each direction, you won’t get any effect of the orientation as it is symmetric.

def create_plot(x, y, nstd=3):
    x, y = np.asarray(x), np.asarray(y)
    cov_matrix = np.cov([x, y])
    eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
    order = eigenvalues.argsort()[0]
    angle = np.arctan2(eigenvectors[1, order], eigenvectors[1, order])

    x0 = np.mean(x)
    y0 = np.mean(y)

    x_dir = np.cos(angle) * x - np.sin(angle) * y
    y_dir = np.sin(angle) * x + np.cos(angle) * y

    w = nstd * np.std(x_dir)
    h = nstd * np.std(y_dir)

    return hv.Ellipse(x0, y0, (w, h), orientation=-angle) * hv.Scatter((x, y))


combined = create_plot(array_0_x, array_0_y) + create_plot(array_1_x, array_1_y)
combined.opts(shared_axes=False)

febedtu · October 12, 2022, 4:03pm

Thank you for the fast response. I really appreciate the help. Unfortunately, there still seems to be an issue with the angle.

Using your code:

def create_plot(x, y, nstd=5):
    x, y = np.asarray(x), np.asarray(y)
    cov_matrix = np.cov([x, y])
    eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
    order = eigenvalues.argsort()[0]
    angle = np.arctan2(eigenvectors[1, order], eigenvectors[1, order])

    x0 = np.mean(x)
    y0 = np.mean(y)

    x_dir = np.cos(angle) * x - np.sin(angle) * y
    y_dir = np.sin(angle) * x + np.cos(angle) * y

    w = nstd * np.std(x_dir)
    h = nstd * np.std(y_dir)

    return hv.Ellipse(x0, y0, (w, h), orientation=-angle) * hv.Scatter((x, y))

c2x = np.random.normal(loc=-2, scale=0.6, size=200)
c2y = np.random.normal(loc=-2, scale=0.1, size=200)

combined = create_plot(c2x, c2y)
combined.opts(shared_axes=False)

bokeh_plot

febedtu · October 12, 2022, 4:18pm

Thank you for the fast response and suggestion. Unfortunately, I accidently did not reply to your comment directly. As I am not sure whether you get any info on indirect replies here, I wanted to let you know that I provided an update above.

Hoxbro · October 12, 2022, 5:00pm

Try to play around with the code yourself. I’m sure you can figure out what is wrong. I have hidden my answer below

My answer

def create_plot(x, y, nstd=5):
    x, y = np.asarray(x), np.asarray(y)
    cov_matrix = np.cov([x, y])
    eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
    order = eigenvalues.argsort()[0]
    angle = np.arctan2(eigenvectors[0, order], eigenvectors[1, order])

    x0 = np.mean(x)
    y0 = np.mean(y)

    x_dir = np.cos(angle) * x - np.sin(angle) * y
    y_dir = np.sin(angle) * x + np.cos(angle) * y

    w = nstd * np.std(x_dir)
    h = nstd * np.std(y_dir)

    return hv.Ellipse(x0, y0, (w, h), orientation=-angle) * hv.Scatter((x, y))


combined = create_plot(array_0_x, array_0_y) + create_plot(array_1_x, array_1_y) + create_plot(c2x, c2y)
combined.opts(shared_axes=False)