I am having problems with geogebra, and thus looked for substitutes.
I found two js libraries KONVA: https://cdn.jsdelivr.net/npm/konva@8/konva.min.js
and JSXGraph https://cdn.jsdelivr.net/npm/jsxgraph/distrib/jsxgraphcore.mjs
of the two, Konva was somewhat easier to handle (although getting the scripts to load proved a pain!)
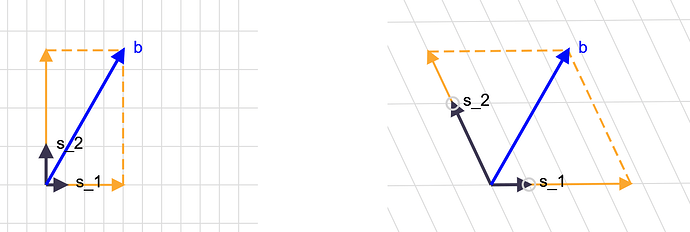
I am appending the same simplistic vector decomposition example for both for comparison.
- KONVA
class VectorDecomposition(JSComponent):
# Parameters
s1 = param.List(default=[1, 0], doc="First basis vector (dx, dy).")
s2 = param.List(default=[0, 1], doc="Second basis vector (dx, dy).")
b = param.List(default=[3, 5], doc="Vector to decompose (dx, dy).")
fixed = param.Boolean(default=False, doc="Disallow moving endpoints of basis vectors.")
vec_name = param.String(default="s", doc="Base name for the basis vectors (e.g., 's' or 'e').")
offset = param.List(default=[100, 100], doc="Offset from the bottom-left corner for the origin (dx, dy).")
_importmap = {
"imports": { # does not seem to work: load in html cell instead!
"konva": "https://cdn.jsdelivr.net/npm/konva@8/konva.min.js",
}
}
_esm = r"""
export function render({ model, el }) {
if (typeof window.Konva === 'undefined') {
throw new Error('Konva is not loaded correctly!');
}
const Konva = window.Konva;
// Create container div
const container = document.createElement('div');
container.style.width = '100%';
container.style.height = '100%';
el.appendChild(container);
// Initialize Konva stage
const stage = new Konva.Stage({
container: container,
width: 400,
height: 400,
});
const offsetX = model.offset[0];
const offsetY = model.offset[1];
const margin = 50; // Margin for padding around the plot
const originX = offsetX + margin;
const originY = stage.height() - offsetY - margin;
// Extract parameters
const s1 = model.s1;
const s2 = model.s2;
const b = model.b;
const fixed = model.fixed;
// Check for vec_name existence
const vec_name = model.vec_name || "s"; // Fallback to "s" if undefined
// Calculate dynamic scaling factor
const maxMagnitude = Math.max(
Math.sqrt(b[0] ** 2 + b[1] ** 2),
Math.sqrt(s1[0] ** 2 + s1[1] ** 2),
Math.sqrt(s2[0] ** 2 + s2[1] ** 2)
);
const availableSpace = Math.min(stage.width() - 2 * margin, stage.height() - 2 * margin);
const scale = availableSpace / (maxMagnitude * 2); // Scale down to fit comfortably
// Layers
const gridLayer = new Konva.Layer();
const vectorLayer = new Konva.Layer();
const controlLayer = new Konva.Layer();
stage.add(gridLayer, vectorLayer, controlLayer);
// ============================================== Helper Functions
function drawGrid() {
gridLayer.find('Line').forEach(line => line.remove()); // Clear grid
const gridSize = 10; // Number of steps in the grid in each direction
for (let i = -gridSize; i <= gridSize; i++) {
for (let j = -gridSize; j <= gridSize; j++) {
const x = originX + i * s1[0] * scale + j * s2[0] * scale;
const y = originY - (i * s1[1] * scale + j * s2[1] * scale);
const parallelToS1 = new Konva.Line({
points: [x, y, x + s1[0] * scale, y - s1[1] * scale],
stroke: '#ddd',
strokeWidth: 1,
});
const parallelToS2 = new Konva.Line({
points: [x, y, x + s2[0] * scale, y - s2[1] * scale],
stroke: '#ddd',
strokeWidth: 1,
});
gridLayer.add(parallelToS1);
gridLayer.add(parallelToS2);
}
}
gridLayer.draw();
}
// ========================================================================
function addLabel(layer, text, x, y, color = 'black') {
const label = new Konva.Text({
text: text,
x: x + 10, // Offset slightly to avoid overlap
y: y - 10,
fontSize: 16,
fontFamily: 'Arial',
fill: color,
});
layer.add(label);
}
// ========================================================================
function drawVectors() {
vectorLayer.find('Arrow, Line, Text').forEach(el => el.remove()); // Clear previous vectors and labels
const s1EndX = originX + s1[0] * scale;
const s1EndY = originY - s1[1] * scale;
const s2EndX = originX + s2[0] * scale;
const s2EndY = originY - s2[1] * scale;
const c = "#3B3651";
const basisVector1 = new Konva.Arrow({
points: [originX, originY, s1EndX, s1EndY],
pointerLength: 10,
pointerWidth: 10,
fill: c,
stroke: c,
strokeWidth: 3,
});
const basisVector2 = new Konva.Arrow({
points: [originX, originY, s2EndX, s2EndY],
pointerLength: 10,
pointerWidth: 10,
fill: c,
stroke: c,
strokeWidth: 3,
});
addLabel(vectorLayer, `${vec_name}_1`, s1EndX, s1EndY, 'black');
addLabel(vectorLayer, `${vec_name}_2`, s2EndX, s2EndY, 'black');
// Target vector (b)
const bEndX = originX + b[0] * scale;
const bEndY = originY - b[1] * scale;
const targetVector = new Konva.Arrow({
points: [originX, originY, bEndX, bEndY],
pointerLength: 10,
pointerWidth: 10,
fill: 'blue',
stroke: 'blue',
strokeWidth: 3,
});
// Add label for b
addLabel(vectorLayer, 'b', bEndX, bEndY, 'blue');
const det = s1[0] * s2[1] - s1[1] * s2[0];
const alpha = (b[0] * s2[1] - b[1] * s2[0]) / det;
const beta = (b[1] * s1[0] - b[0] * s1[1]) / det;
const alphaX = originX + alpha * s1[0] * scale;
const alphaY = originY - alpha * s1[1] * scale;
const betaX = originX + beta * s2[0] * scale;
const betaY = originY - beta * s2[1] * scale;
const alphaVector = new Konva.Arrow({
points: [originX, originY, alphaX, alphaY],
pointerLength: 10,
pointerWidth: 10,
fill: 'orange',
stroke: 'orange',
strokeWidth: 2,
});
const betaVector = new Konva.Arrow({
points: [originX, originY, betaX, betaY],
pointerLength: 10,
pointerWidth: 10,
fill: 'orange',
stroke: 'orange',
strokeWidth: 2,
});
const alphaToB = new Konva.Line({
points: [alphaX, alphaY, bEndX, bEndY],
stroke: 'orange',
strokeWidth: 2,
dash: [10, 5],
});
const betaToB = new Konva.Line({
points: [betaX, betaY, bEndX, bEndY],
stroke: 'orange',
strokeWidth: 2,
dash: [10, 5],
});
vectorLayer.add(alphaToB, betaToB, alphaVector, betaVector, basisVector1, basisVector2, targetVector);
vectorLayer.add(basisVector1, basisVector2);
vectorLayer.add(targetVector);
addLabel(vectorLayer, `${vec_name}_1`, s1EndX, s1EndY, 'black');
addLabel(vectorLayer, `${vec_name}_2`, s2EndX, s2EndY, 'black');
addLabel(vectorLayer, 'b', bEndX, bEndY, 'blue');
//addLabel(vectorLayer, `α=${alpha.toFixed(2)}`, alphaX, alphaY, 'orange');
//addLabel(vectorLayer, `β=${beta.toFixed(2)}`, betaX, betaY, 'orange');
vectorLayer.draw();
}
// ========================================================================
function drawControlPoints() {
controlLayer.find('Circle').forEach(el => el.remove());
if (fixed) return;
const s1Control = new Konva.Circle({
x: originX + s1[0] * scale,
y: originY - s1[1] * scale,
radius: 6,
fill: null,
stroke: 'lightgray',
draggable: !fixed,
});
const s2Control = new Konva.Circle({
x: originX + s2[0] * scale,
y: originY - s2[1] * scale,
radius: 6,
fill: null,
stroke: 'lightgray',
draggable: !fixed,
});
controlLayer.add(s1Control, s2Control);
if (!fixed) {
s1Control.on('dragmove', () => {
s1[0] = (s1Control.x() - originX) / scale;
s1[1] = (originY - s1Control.y()) / scale;
gridLayer.destroyChildren();
drawGrid();
drawVectors();
});
s2Control.on('dragmove', () => {
s2[0] = (s2Control.x() - originX) / scale;
s2[1] = (originY - s2Control.y()) / scale;
gridLayer.destroyChildren();
drawGrid();
drawVectors();
});
}
controlLayer.draw();
}
// ========================================================================
// Initial draw
drawGrid();
drawVectors();
drawControlPoints();
}
"""
- JSXGraph
class JXG_VectorDecomposition(JSComponent):
"""
A JSXGraph-based component to visualize vectors s1 and s2.
"""
# Parameters
origin = param.List(default=[0, 0], doc="Origin of the plot (x, y).")
s1 = param.List(default=[1, 0], doc="First basis vector (dx, dy).")
s2 = param.List(default=[0, 1], doc="Second basis vector (dx, dy).")
b = param.List(default=[4, 7], doc="Vector to decompose (dx, dy).")
fixed = param.Boolean(default=True, doc="Disallow moving endpoints of basis vectors.")
vec_name = param.String(default="s", doc="Base name for the basis vectors (e.g., 's' or 'e').")
_esm = r"""
import JXG from 'https://cdn.jsdelivr.net/npm/jsxgraph/distrib/jsxgraphcore.mjs';
import MJAX from 'https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-chtml.js';
export function render({ model, el }) {
// Create a div element to hold the JSXGraph board
let boardDiv = document.createElement("div");
boardDiv.style.width = "300px";
boardDiv.style.height = "300px";
el.appendChild(boardDiv);
// Global JSXGraph options for rendering
JXG.Options.label.autoPosition = true;
JXG.Options.text.useMathJax = true;
JXG.Options.text.fontSize = 20;
// Extract parameters
const origin = model.origin;
const s1 = [...model.s1];
const s2 = [...model.s2];
const b = [...model.b];
const fixed = model.fixed;
const baseName = model.vec_name;
// =========== Initialize the JSXGraph board ======================================
let board = JXG.JSXGraph.initBoard(boardDiv, {
boundingbox: [-5, 5, 5, -5],
showCopyright: false, showNavigation: false, axis: false });
// Create a fixed invisible point at the origin
const originPoint = board.create('point', origin, {
name: '',
visible: false,
fixed: true,
});
// Store gridlines and decomposition arrows for clearing before redraw
let gridlines = [];
let decompositionArrows = [];
// =========== Function to Draw Gridlines =========================================
function draw_gridlines(s1, s2, range = 12, color = '#ccc') {
// Clear existing gridlines
gridlines.forEach((line) => board.removeObject(line));
gridlines = [];
// Generate gridlines parallel to s1
for (let i = -range; i <= range; i++) {
const offsetX1 = i * s2[0];
const offsetY1 = i * s2[1];
const line = board.create('line', [
[origin[0] + offsetX1, origin[1] + offsetY1],
[origin[0] + offsetX1 + s1[0], origin[1] + offsetY1 + s1[1]]
], { strokeColor: color, dash: 2, fixed: true });
gridlines.push(line);
}
// Generate gridlines parallel to s2
for (let i = -range; i <= range; i++) {
const offsetX2 = i * s1[0];
const offsetY2 = i * s1[1];
const line = board.create('line', [
[origin[0] + offsetX2, origin[1] + offsetY2],
[origin[0] + offsetX2 + s2[0], origin[1] + offsetY2 + s2[1]]
], { strokeColor: color, dash: 2, fixed: true });
gridlines.push(line);
}
}
// =========== Function to Draw Arrows =========================================
function draw_arrow(endpoint, color, fixed, onUpdate = null, baseName=null) {
const endPointCoords = [origin[0] + endpoint[0], origin[1] + endpoint[1]];
let endPoint = null;
if (!fixed) { // Create a visible and draggable endpoint if the vector is not fixed
endPoint = board.create('point', endPointCoords, {
name: '', visible: true, fixed: false, size: 3, fillColor: color, strokeColor: color, });
endPoint.on('drag', function () { // Add interactivity if the endpoint is movable
const newEndpoint = [endPoint.X() - origin[0], endPoint.Y() - origin[1]];
onUpdate && onUpdate(newEndpoint); // Call onUpdate if provided
});
} else { // Use a non-interactive virtual point for fixed vectors
endPoint = board.create('point', endPointCoords, {
name: '', visible: false, fixed: true, });
}
// Draw the arrow from the origin point to the endpoint and return it
const arrow = board.create('arrow', [originPoint, endPoint], {
strokeWidth: 2, strokeColor: color, });
if (baseName) { // Add a label to the arrow if baseName is provided
board.create('text', [ // Create a dynamic label whose position updates with the arrow
function () {
return (originPoint.X() + endPoint.X()) / 2 - 0.5;
},
function () {
return (originPoint.Y() + endPoint.Y()) / 2 - 0.5; // Midpoint Y, slightly offset above the arrow
},
`\\(\\vec{${baseName}}\\)`
], {
anchorX: 'middle',
anchorY: 'middle',
useMathJax: true,
});
}
return arrow;
}
// =========== Function to Decompose and Draw Arrows ==============================
function draw_decomposition(s1, s2, b) {
// Clear existing decomposition arrows
decompositionArrows.forEach((arrow) => board.removeObject(arrow));
decompositionArrows = [];
const denominator = s1[0] * s2[1] - s1[1] * s2[0];
if (denominator === 0) {
console.error("Vectors s1 and s2 are linearly dependent. Decomposition not possible.");
return;
}
const alpha = (b[0] * s2[1] - b[1] * s2[0]) / denominator;
const beta = (b[1] * s1[0] - b[0] * s1[1]) / denominator;
const alphaS1 = [alpha * s1[0], alpha * s1[1]];
const betaS2 = [beta * s2[0], beta * s2[1]];
const bCoords = [b[0], b[1]];
const color="green";
// Draw arrows for alpha s1 and beta s2 and add them to decompositionArrows
decompositionArrows.push(draw_arrow(alphaS1, color, true));
decompositionArrows.push(draw_arrow(betaS2, color, true));
// Draw arrows from alpha s1 to b and beta s2 to b and add them to decompositionArrows
const arrow1 = board.create('arrow', [
[origin[0] + alphaS1[0], origin[1] + alphaS1[1]],
[origin[0] + bCoords[0], origin[1] + bCoords[1]],
], { strokeColor: color, strokeWidth: 2, fixed: true });
const arrow2 = board.create('arrow', [
[origin[0] + betaS2[0], origin[1] + betaS2[1]],
[origin[0] + bCoords[0], origin[1] + bCoords[1]],
], { strokeColor: color, strokeWidth: 2, fixed: true });
decompositionArrows.push(arrow1);
decompositionArrows.push(arrow2);
}
// =========== Draw Arrows and Attach Interactivity ================================
let currentS1 = [...s1];
let currentS2 = [...s2];
draw_arrow(b, "blue", true, null, 'b');
// Draw initial gridlines and decomposition
draw_gridlines(s1, s2);
draw_decomposition(s1, s2, b);
draw_arrow(s1, "#60708B", fixed, (newEndpoint) => {
currentS1 = newEndpoint;
draw_gridlines(currentS1, currentS2); // Update gridlines when s1 changes
draw_decomposition(currentS1, currentS2, b); // Update decomposition when s1 changes
}, baseName+'_1' );
draw_arrow(s2, "#60708B", fixed, (newEndpoint) => {
currentS2 = newEndpoint;
draw_gridlines(currentS1, currentS2); // Update gridlines when s2 changes
draw_decomposition(currentS1, currentS2, b); // Update decomposition when s2 changes
}, baseName+'_2' );
// =========== Cleanup when the component is removed ==============================
model.on('remove', () => {
//console.log("JSXGraphComponent removed.");
JXG.JSXGraph.freeBoard(board);
});
}
"""