Interactive plot of weather data on an unstructured grid

HoloViews
1

Hey everyone,
I just started to get into Holoviews and had already some good fun with experimenting with some ICON data.

I’ve got the current task now to make an interactive plot of the date where it’s possible to see the change in time or height.
So far I was able to either make a static plot (no variation in height or time) or make an interactive plot, but there I wasn’t able to get the the TriMesh and the projection working. Has anyone an Idea how to solve that issue? Or is there a way to have a DynamicPlot in a Dynamicplot?

import cartopy.crs as ccrs
import cartopy.feature as cf
import datashader as ds
import geoviews as gv
import geoviews.feature as gf
import holoviews as hv
import numpy as np
import pandas as pd
import xarray as xr
from holoviews import opts
from holoviews.operation.datashader import datashade, rasterize, regrid
from scipy.spatial import Delaunay
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
import matplotlib.pyplot as plt

datashade.precompute = True

hv.extension("bokeh")

def merge(data_file, grid_data, path = './'):
    """
    Merging the data with the grid file and returs the merged x-array
    args: data x-array, grid x-array
    returns: merged x-array
    """
    
    data = xr.open_dataset(path+data_file)
    grid_data = xr.open_dataset(path+grid_data)
    
    return xr.merge([data.rename({'ncells': 'cell'}), grid_data])




def triangulate(vertices, x="Longitude", y="Latitude"):
    """
    Generate a triangular mesh for the given x,y,z vertices, using Delaunay triangulation.
    For large n, typically results in about double the number of triangles as vertices.
    """
    triang = Delaunay(vertices[[x, y]].values)
    return pd.DataFrame(triang.simplices, columns=['v0', 'v1', 'v2'])




def calc(pressure):
    pts = np.stack((x, y, pressure)).T
    verts = pd.DataFrame(pts, columns=['Longitude', 'Latitude', 'pres'])
    tris = triangulate(verts)    
    return verts, tris

data_file = "20200404_12_ana.nc"
grid_data = "icon_grid.nc"

data = merge(data_file, grid_data)
data = data.isel(time=0)

x = ((np.rad2deg(data.clon) - 180) % 360) - 180
y = np.rad2deg(data.clat)
data

data_out
data_out865×406 24 KB 

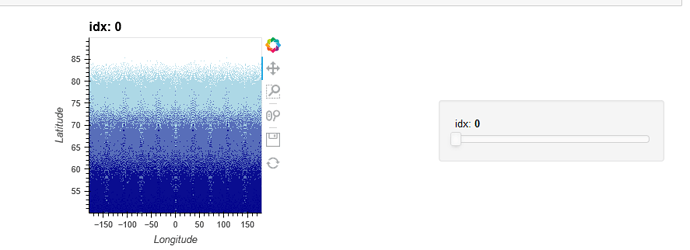
def points(idx, data = data):
    verts, tris = calc(data.pres[idx])
    return rasterize(hv.Points(verts, vdims='pres'), dynamic = False)
    #return hv.TriMesh(rasterize(hv.Points(verts, vdims='pres'), dynamic = False)) <- not working

img = datashade(hv.DynamicMap(points, kdims=['idx']))
img.redim.range(idx=(0,69))

with slider
with slider887×322 22 KB

following followed by source

graticules = cf.NaturalEarthFeature(
    category='physical',
    name='graticules_30',
    scale='50m')

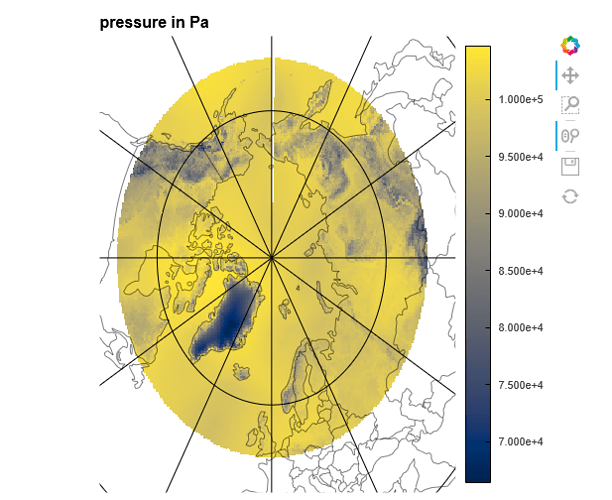
verts, tris = calc(data.pres[-1])
trimesh = rasterize(
    gv.TriMesh(
        (tris, hv.Points(verts, vdims='pres')),
        label="pressure in Pa",
        crs=ccrs.PlateCarree(),
    ),
    aggregator=ds.mean('pres'),
)
(trimesh).opts(
    colorbar=True, alpha = 0.99, cmap = 'cividis',width=500, height=500, projection=ccrs.NorthPolarStereo()
) * gf.coastline * gf.borders * gv.Feature(graticules, group='Lines')

plot
plot617×504 146 KB

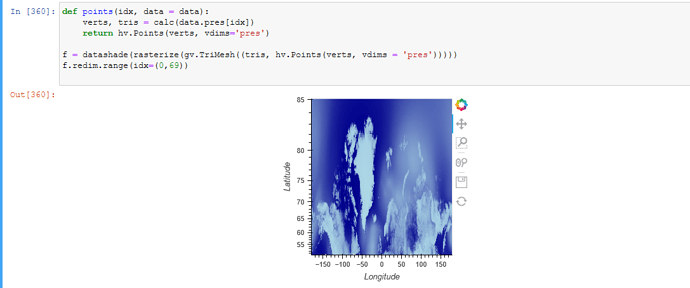
I also managed to do this, but got stuck there: (animation still doesn’t work)

anothertryPNG
anothertryPNG1087×455 87.9 KB

2

I figured out how to get the plot interactive in case anybody is interested, but still struggling with the projection and also trying to optimize the calculation time bc it takes a couple of seconds for each frame.

(using the calc function and the data set as shown above)

cvs = ds.Canvas(plot_height=400,plot_width=400)
def func(idx, data = data): 
    ver, tri = calc(data.pres[idx])
    mesh = du.mesh(ver,tri)
    obj = tf.shade(cvs.trimesh(ver, tri, mesh = mesh, interpolate='linear')).to_pil()
    plot = hv.RGB(np.array(obj))#, bounds=(-10,-10,10,10))
    return plot
    
shade = datashade(hv.DynamicMap(func, kdims=['idx'])).opts(alpha = 0.99, projection=ccrs.NorthPolarStereo()) * gf.coastline * gf.borders * gv.Feature(graticules, group='Lines')
shade.redim.range(idx=(0,69))

interactive
interactive1080×333 95.8 KB

3

if anyone is interested, here is a proper solution for the animation. Just improved the calc function as well, but this one works as well :slight_smile:

def f(idx, data=data):
    ver, tri = calc(data.pres[idx])
    points = gv.operation.project_points(gv.Points(ver, vdims=['pres']))
    trimesh = gv.TriMesh((tri, points),crs=ccrs.Mercator())
    return trimesh

s = datashade(hv.DynamicMap(f,kdims = ['idx'])).opts(alpha = 0.8, projection=ccrs.NorthPolarStereo()) * gf.coastline * gf.borders * gv.Feature(graticules, group='Lines')
s.redim.range(idx=(0,69))
1 Like